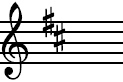Borrowed Chords and Secondary Dominants: The Secret Ingredients of Chord Progressions

In the last post we discussed the concept of chord progressions and how the individual chords in the sequence are related to each other. Today I want to talk about chords in a progression that fall outside the standard key signature of the piece, particularly borrowed chords and secondary dominants.

A borrowed chord, is a chord in a progression that is taken from the parallel key (the minor or major scale with the same tonic). An example of a parallel key would be (Cmin) in relation to (Cmaj). Both scales in their respective keys start with (C), hence (C) is the tonic of both keys, making them parallel in structure. A piece of music using borrowed chords uses this parallel structure to provide variety and a different "feel" to the song. For example, the song "Happy Together" by the Turtles uses borrowed chords to change the song from major to minor between the chorus and the verse. Listen to the song below and see if you can hear the spots in which chords are taken out of the original key:

The next concept I want to talk about is that of secondary dominants. As we know from a previous post, the dominant of key is the fifth triad above the tonic. So if we are in the key of C major, the dominant triad is G major. As discussed in last weeks post there is a very strong relationship between the dominant and the tonic, so much so that many cadences (chord progressions that bring about the end of a musical phrase) are centered around them. So we know what the "dominant" is, but what does the "secondary"part mean? Let's look at an example of a chord progression that uses a secondary dominant to see if we can find out. 

I apologize for the poor quality of the picture, but this is a perfect example of a secondary dominant chord used in the key of C Major. Here we see that the piece starts on the tonic (C), then goes to the subdominant or the Four Chord (F). After the four chord however, something happens that gives us a D Major chord before going to the dominant (G) and resolving with the tonic (C). What is going on? 

This is what is known as a secondary dominant. As defined it is the use of the dominant "of the dominant" of the set key. So if the set key in this case is (C major) the dominant is (G major) and the dominant of that is (D Major). If you have a piano this relationship can be seen my going up two fifth intervals from C. (C --> G --> D). In the key of G major the dominant is D Major (because in G major the F is sharp) and this gives us a chord that is taken outside of its original key but is related to the dominant of the key the piece is played in. 

Secondary dominants can be used in different ways throughout music, and it does not always have to be the dominant of the dominant. You can have a secondary dominant that is based off the (ii) chord in a piece, such as what is used in "Tears of Heaven" by Eric Clapton, or one that is taken from the (Vi) chord as in "Yesterday" by the Beatles. Here is an example of a chord progression that implements secondary dominance:   

In a couple days I will post a follow-up post that has a couple more examples of borrowed chords and secondary dominants, as this was meant to be an introduction to the concept. If you have any comments or questions then please post below, but other than that thank you for reading!

-Sincerely, ZS

Diatonic Chord Progressions: The Baseline of Songwriting

Today we're going to talk about a subject that is very dear to my heart: Chord Progressions and how they relate to songwriting. If you've ever had the dream of becoming a songwriter and given up after little success, there are three things that probably got in your way of becoming famous.

 First of all, as my rhyming dictionary loves to remind me, writing good lyrics takes time and patience to master. Whether you become inspired to write a lyric or it just comes to you in the middle of the night, lyrics need to be refined and practiced in order to be "good". Now "good" is a flexible term because the quality of the lyrics all depends on your audience. Are you writing for the opening of the next concert center in your city, or for personal enjoyment?

This brings us to my second point. Self-confidence is needed in order to be a good writer. The ability to write down a couple lines of lyrics or a measure of melody and be *ok* with what you wrote the next morning is a skill that even I haven't learned yet. The important thing to remember is that no matter what you write down, you need to KEEP IT. Get a journal, take a note on your iPhone, or record it somehow, but don't just throw it away. Keeping ideas around, even if you think it's garbage, will stand as a milemarker to how far you have come as a write, and might even inspire you later on through the words that once didn't.

Finally, and most importantly, beginning song writers don't have a firm concept of chord progressions. To clarify, a chord progression is a series of music chords or notes with the goal of establishing a tonality within a specific key and is based on the succession of root relationships. Big definition right? Let's break this down in todays video, and then apply it to some popular songs so we can understand, as music writers, the fundamentals of chord progressions.

To start with, lets understand that today will only be spent discussing diatonic chord progressions. This means that all the triads and chords we will build our progression from will be within the same key. This means that if we want to make a progression in which the root, or tonic, is in the key of C, we will not find chords that are out of this key (such as Ab or Cm).

Diatonic Chords in the key of C Major

(the 2, 3, and 6 of this progression are minor, meaning that the roman numerals should have lower case (i's))

In the picture above the following chords are shown in the key of C major:

   I                 ii                  iii                   IV                        V                   Vi               Vii diminished
tonic      supertonic      mediant       subdominant         dominant       submediant            subtonic

As stated before, a chord progression is a series of of chords, so we know that in order to create a progression we're going to have to put these chords in some sort of order. But wait, is it really that simple? Well....yes. There are no set rules as to what chords follow others in a chord progression. This leaves room for creativity within compositions so we aren't constrained to a few styles of progressions. That being said, there are guidelines for deciding what chords should follow others in a chord progression.

Typically, root relationships revolved around the distances that chords have from each other. This distance is based from the interval space between the tonic (1st) note of each triad. For example, the root relationship between the (I) and the (iii) chord in the key of C Major is a major 3rd. This is because the root of the (I) chord is (C), and the distance between it and the root of the (iii) chord, (E), is a major third.

These types of relationships form strong connections between chords. In classical music the relationship between the (V) and the (I) chord is important in the context of many cadences. A cadence is a harmonic configuration which gives the phrase of music a sense of resolution or pause. Another relationship in chord progressions that can be heard is the (IV) to (I) cadence, which is often displayed in Church Music as the "A-men" phrase at the end of a prayer.

Lets now apply this to a song that I am currently singing in my Concert Choir.

*Note: This piece is in the key of E Major*

The focus of this picture is the cadence that occurs at the end of the crescendo ("home"). As a baritone, my line goes from an (E) to a (B), which is a 4th interval. But look at the other parts. If we connect the notes that the composer spread throughout the voice parts, then we end up with a (E6) and a (B) Chord. The relationship between these chords is a 4th, but because the piece is in E major this transition is from the tonic chord (I) down to the Dominant (V) if gives the phrase a sense of continuation. Instead of simply ending the phrase and moving on to the next musical idea, this composer decides to create anticipation within the music that brings about the main focus of the piece. 

Let's now look at the opposite within the same piece. 

This is a measure from a later section of the piece in which a cadence is used to end the phrase. Here, the notes I sing in the bass line still have the 4th relationship. The two chords (A6) and (E) also share this relationship. Now if you think about the two cadences we've looked at so far, you'll notice they they both incorporate movement in 4ths. But in the first cadence a 4th is used to introduce a new phrase by going down in tonal movement from the tonic to the dominant, while the second moves down from the subdominant to the tonic. By returning to the tonic chord it brings the phrase to a sense of closure, allowing the music to shift focus or enforce another idea. 

So through these examples we see the affect of movement between the chords. Movement away from the tonic, or any chord really, can have different affects on the music depending on if they're moving up or down the diatonic scale. Through this method, ideas in the music can be expressed as transitions or closing statements, all while using the same relationships between the chords. 

Thanks for reading and if you have any questions about the concept of root relationships and movement let me know by commenting on the post below!

Sincerely, ZS 

Instructional Methods: 7th Chords

Today we're going to do something a little different. As you should know if you read the introduction to this site in my first post, I'm a Music Education major. While this site is doing wonders for helping me apply the knowledge I learn in class, it is also assisting me in refining my teach strategies. So in this post we're going to focus on the "educational" element of music theory.

Posted below is a video from YouTube that explains the concept of 7th chords. Watch it, and then we'll discuss it below. 

Alright. Let's break this teaching style down before we discuss the concept of 7th chord structure ourselves. 

In this video, the whiteboard behind the instructor is used as a visual tool for the students (audience). This is helpful because now we can physically "see" the examples that the instructor gives to break down the lesson. Now, I'm not a huge fan of how fast he speaks in the video, but it's compensated in the end as he does provide a summary of the concepts he covers. 

Moving on to the actual method of teaching he implements in the video, I have mixed feelings about his "Scale Method" in describing the structure of 7th chords. While he is correct in saying that the seventh chord is composed of the 1st, 3rd, 5th, and 7th degrees of a scale, he fails to describe the relationship between the individual notes. Don't get me wrong, this is a excellent video for those that want a basic understanding of what 7th chords are and how to construct them, but fails to give insight as to "why" the chords sound the way they do. 

Seventh chords are essentially triads with the seventh scale degree played with them (He addresses this in the video). From the previous post we know that there are four different types of triads: Major, Minor, Augmented, and Diminished. These triads are created by manipulating the intervals that compose them (between major and minor). A similar concept is used in creating seventh chords. 

We know that triads are composed of three notes, and two intervals of 3rd's describe the relationship between the 1st and 3rd, and 3rd and 5th scale degrees. So, like the video says, to create a seventh chord we add the seventh scale degree on top of the triad. It's important to notice that the interval between the 5th and the 7th degree is also a third. Knowing this, we see a pattern of 3rds between each note. 

Let's look at an example: 

The chord to the left is a C Major 7th Chord. Notice that the relationship between each note and the note that immediately follows it is a 3rd. The resulting chord is composed of a triad (C E G) and a seventh interval (Between C and B). 

As you hopefully know, there are different types of seventh chords. These different chords are created by changing the type of triad along with altering the form of 7th interval on top of it. These details will be expanded on me in a later post. 

So overall, how can we summarize this instructors method? 

Good:

-Things on the board are written out and clear 

-Has his own method of instruction that is easy to understand

Bad:

-Speech is a little rushed and there is little review between steps, making the lesson hard to follow 

-The relationship between the notes in a seventh chord is not explained

-Skips around (whether by poorly editing the video or otherwise) to deliver a concept of seventh chords that cannot be expanded into physical musical notation. 

Again, this portion of the post is more for my benefit then anyone else's, as I'm trying to be analytical with instructional methods. If you feel I overlooked something, or didn't give a clear definition of your basic seventh chord, then please let me know so I can go back and explain it in more detail. 

Thanks for reading!

Sincerely, ZS 

Enharmonic Notes and Key Signatures

      What is a Key Signature? What are accidentals? How is it possible for a note like (C) to have more than one name?

      Let's start with the basics. We know that notes (or pitches as some might refer to them), arrange themselves onto the master staff as displayed below.

          But what most beginning instrumentalists and singers don't understand is that there is a lot of space between each note on the staff. For example, between the notes (C) and (D) is the note (C#) right? And between (A) and (B) is (Bb) right? If you play the piano, you know these notes exist because they are represented by the black keys that sit in between the white keys.  

     So what is meant by the Sharp/(#) symbol? A sharp is a type of accidental that means to play the respective note "up" one semitone (or half-step). So if we drew a sharp next to a (C) on the scale, we would now call this note (C Sharp)/(#C). 

      What about the Flat/(b) symbol? A flat is another type of accidental that means the play the respective note "down" one semitone (or half-step). So if we drew a flat next to a (E) on the scale, we would now call this note (E Flat)/(Eb) 

But wait a second, the black keys in the picture have two names! How is that possible, and how do you know which name to call each note if they have more than one? 

           ^The question above brings up a good point. The black keys have more than one name for each note, and which name to call them all depends on what note you're using as a reference point. If a pitch can be represented by different names and different accidentals, then it can be labeled as enharmonic. For example, (D#) is the same as (Eb) because the raising of (D) one semitone or the lowering of (E) one semitone results in the same pitch. Now, how you know which name to call notes depends on the key signature you're in. 

           But without worrying about when to call which notes what, let's talk about how notes can have different names. First of all, it's important to remember that enharmonic names can only be given off the primary tones (my way of saying the "white keys"). So this means you cannot have a note called (F# sharp) or (Eb Flat). These notes *can* be expressed by other notes, but not by "black keys". 

The note (G) can be expressed from the note (F) by an accidental known as a Double Sharp (x). Instead of the note being raised "one" semitone, it is now raised "two" semitones. So (Fx) is another way of saying (G). 

      The note (G) can also be expressed from the note (A) by an accidental known as a Double Flat (bb). Now, instead of the note being lowered "one" semitone, it is lowered "two" semitones. So (Abb) is another way of saying (G). In this way we now have three names for (G). Most all of the pitches on the keyboard have three names except for one, which only has two. (see if you can figure out which one). 

      Anyway, let's now move along and talk about Key Signatures so we can tie in these note names with how they are expressed in different keys. 

Key Signatures are collections of accidentals (sharps and flats) that are found in specific scales (We'll talk about scales in more detail Friday). Key signatures are used in music because they eliminate the need to write out all the individual sharps and flats that unique scales are formed by. Let's analyze a couple examples for absolute clarity on this topic;

The key signature shown to the right is F Major. Note that a flat is drawn on the (B) line on the treble clef. This means that when notes are placed on that clef they are automatically played one semitone below the standard (B). So if a note was drawn on that line, we would call that note (Bb), even though no accidentals are written directly in front of the note, because of the key signature. 

The key signature to the right is Bb Major (We will discuss identifying key signatures at the end of the post). Keep in mind that any notes placed on the (B) line will still be flattened because of the accidental in the key signature, but now we're going to add another line that follows this same method: (E). Now if a note is drawn on either the (B) or (E) line, we know to flatten that note automatically. 

Does this make sense for the flats? I'm going to move on to some key signature that have sharps in them, but if you don't have a firm grasp on this concept, go to this site: Key Signature Help

The Key Signature to the left is G Major. Notice that a sharp has a been drawn on the (F) line in the treble clef. Because this accidental has been written on this line, all notes that will be one the (F) line will be "raised" one semitone (half-step). So if a note was drawn on the (F) line, we would call it (#F). 

The Key Signature to the left is D Major. Notice that an accidental has been placed on the (C) line, in addition to the one on the (F) line. Now, if a note is placed on the (C) line, we know to "raise" it a half-step along with any notes drawn on the (F) line. 

The purpose of these examples was to demonstrate how pitch notation is affected by key signatures. Keeping key signatures in mind, it removes the need to mark accidentals next to each note that is played above or below pitch in different key signatures. This is really setting the stage for the next post on my blog which will be about Scales and Relative Key Signatures, but it's nice to have this information now so we can apply it to the basic principles of Enharmonic Notes. 

Typically, we will define enharmonic notes by the key they are played in. For example, a (F#) will be known as F Sharp in the key of D Major because it's a sharp that's written on the staff. The same goes for (C#). 

Likewise, if we wanted to know whether to call a note (Bb) or (A#), we would look at the key signature. If the key was F major, then it would be called (Bb). 

Now, as you've probably guessed, there are more key signature than just the one's I've used as examples. Here's a picture that shows all of them. 

How do we identify these key signatures? Well, the process is actually a lot easier than it looks. This is because there are some simple tricks within the accidentals that help to identify these signatures. 

For flats: Look at the second to last flat. Identify what line it's on and the key signature is the flattened note on the line (Always major). 

For Sharps: Look at the last sharp in the sequence. Raise that not up an additional half-step and you'll have your major key. 

Notice that these rules apply for every signature except for C Major and F Major (Due to the lack of accidentals or two flats) Sadly, you have to memorize these, but it's a lot better than memorizing all TWELVE.

So tying this back to what we learned earlier, Key signature's allow musicians to write music without having to specify the accidentals of each note. There is one exception to this rule, where a note is written into the score that is indicated as sharp/flat, but is played "as written", meaning it is played without any sharps or flats. This is what the "natural" symbol looks like:
  

The last thing I want to talk about in this post is how notes retain their accidental properties till the end of the measure. As we know, key signatures allow notes to be written with their accidentals "implied" by the line or space they are drawn in. But what if we have a note that is out of the key such as a double flat/sharp or natural? Does that note retain it's new properties for the rest of the piece?

The answer is no. If a key signature indicates that a note is always played flat, then it will always be played this way "unless" specified differently. At the end of the measure that the difference occurred however, the note reverts back to it's form as instructed by the key signature. 

For example, let's pretend this measure to the right is in a key which specifies the note (A) to be flat. Now, we see that after the (C#) the (A) appears again, but this time it's (A) natural. So the difference between (Ab) and (A) natural is one half-step up. At the beginning of the next measure if (A) was to be played again, it would return to it's flattened form.





I'll post a couple examples of this later this week to provide clarity, but if you have any questions that I didn't address in the post feel free to comment below!

Sincerely, ZS